Page 63 - sjsi

Research Article: Tawashi & AlAmoudi 63

function of the relative strain according to

the following:

= [ ] (4)
)
′ ( −1)+(

= 0.058. ′ + 1

He also presented a mathematical formula.
Equation 5. in order to calculate the strain of
concrete as a function of the maximum
compression strength in the concrete:
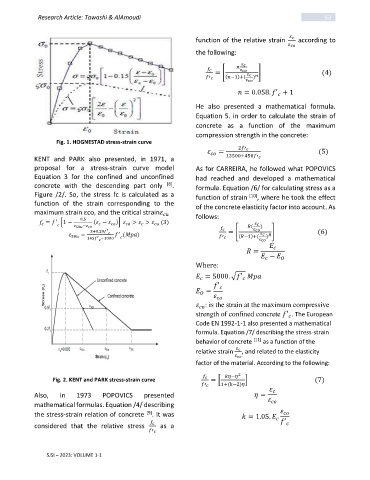
Fig. 1. HOGNESTAD stress-strain curve
= 2 ′ (5)
KENT and PARK also presented, in 1971, a 12500+450 ′
proposal for a stress-strain curve model As for CARREIRA, he followed what POPOVICS
Equation 3 for the confined and unconfined had reached and developed a mathematical
concrete with the descending part only [8] . formula. Equation /6/ for calculating stress as a
Figure /2/. So, the stress fc is calculated as a function of strain [10] , where he took the effect
function of the strain corresponding to the
of the concrete elasticity factor into account. As
maximum strain εco, and the critical strain follows:
0.5
′
= [1 − 50 − ( − )] > > (3) ( )

3+0.29 ′ ′ = [ ] (6)
50 = ( ) ( −1)+(
)
′
145 −1000 ′

=
−

Where:
= 5000. √ ′

′
=

: is the strain at the maximum compressive

strength of confined concrete ′ . The European

Code EN 1992-1-1 also presented a mathematical
formula. Equation /7/ describing the stress-strain
behavior of concrete [11] as a function of the
relative strain , and related to the elasticity

factor of the material. According to the following:
Fig. 2. KENT and PARK stress-strain curve = [ − 2 ] (7)
′ 1+( −2)
Also, in 1973 POPOVICS presented =

mathematical formulas. Equation /4/ describing
[9]
the stress-strain relation of concrete . It was = 1.05.
considered that the relative stress as a ′
′

SJSI – 2023: VOLUME 1-1